Statistiques en SVG avec Python

04/11/2004

XML a apporté son lot de nouvelles applications. SVG est l’une d’entre elles. SVG permet de faire du dessin vectoriel de façon très simple et sans librairie particulière puisqu’il s’agit d’un format XML. Nous allons voir comment utiliser la puissance de python pour collecter des informations sur la taille des répertoires d’un disque et générer un graphique à base d’histogrammes représentant les résultats.
(Login: n°121, novembre 2004 – Frédéric Laurent)

La figure 1 offre un aperçu du diagramme SVG d’occupation du disque que nous obtiendrons avec notre court exemple Python. Pour un répertoire et une profondeur donnés (ici le répertoire c:\Python et une profondeur 2), le graphique permettra de comprendre quels sont les répartitions en termes de pourcentage des différents répertoires contenus dans le chemin initial.

[fichier SVG]

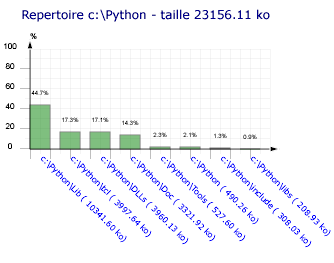
Figure 1: Statistiques de l’occupation de la
distribution python

Pour construire un tel graphique, le programme se divise en deux parties. La première permet d’explorer le système de fichiers et de collecter les informations de tailles des répertoires. La seconde partie met en forme ces données. Pour arriver à nos fins simplement, rien de tel qu’un papier quadrillé et un crayon. Il va nous servir à construire très simplement le repère et l’enchaînement des différents rectangles représentant les valeurs en pourcentage de l’espace occupé sur le disque.

Histoire de repères

Le système de coordonnées de SVG est assez classique en informatique. Le point (0,0) se trouve en haut à gauche. L’axe des abscisses croît de gauche à droite et l’axe des ordonnées croît de haut en bas. La figure 2 illustre ce système.

[fichier SVG]

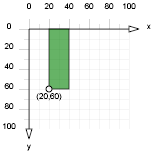
Figure 2: Système
de coordonnées SVG

S’il est courant de rencontrer cette orientation, elle rentre cependant en opposition avec les habitudes prises sur les bancs de l’école. Ainsi, nos souvenirs de mathématiques nous conduisent à réfléchir avec un système un peu différent. Inventé au 17ème siècle par René Descartes, le système cartésien situe l’origine vers le bas de l’écran et si l’orientation de l’axe des abscisses ne changent pas, celui des ordonnées se retrouve inversé, comme l’illustre la figure 3.

[fichier SVG]

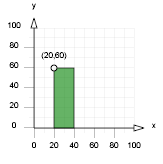
Figure 3: Système de
coordonnées cartésien

Alors comment passer de l’un à l’autre ? Comment réfléchir avec un repère cartésien et avoir un graphique correct ? Deux solutions sont envisageables. La première consiste à concevoir une fonction au niveau du langage de programmation qui fera la conversion des points exprimés dans le système cartésien en des points corrects dans le système de coordonnées de SVG. La seconde utilise les coordonnées cartésiennes directement dans le document SVG et définit les transformations à appliquer sur les éléments graphiques pour obtenir le résultat attendu. Nous allons opter pour la seconde solution. La première transformation fera donc une translation (fonction translate) de tous les points vers le bas. Nous utilisons une translation (30,130) qui correspond à une première translation de (30,30) pour éloigner le graphique du bord du document, à laquelle s’ajoute une translation de (0,100). 100 étant la valeur maximale des ordonnées.

Ensuite, il faut inverser l’axe des ordonnées en l’orientant de bas en haut. La fonction scale qui permet d’appliquer à chaque point un facteur multiplicatif. scale(1,-1) appliqué à chaque point permet de conserver l’abscisse et inverse l’ordonnée. Au niveau du document SVG, un simple bloc englobant permet d’appliquer les transformations à tous les composants graphiques situés à l’intérieur de ce bloc :

<g transform="translate(30,130) scale(1,-1)">
  <rect .../>
  <line .../>
</g>

Scalable Vector Graphics

Scalable Vector Graphics (SVG) est un langage XML, né en 1998 peu après la recommandation XML 1.0. Il est issu d’un groupe de travail du W3C. Il permet de …(lire la suite)

L’attribut transform définit la séquence des transformations. Elles sont définies les unes à la suite des autres en les séparant par un espace.

Simple, mais…

Cette transformation globale a l’avantage d’être simple, mais elle inverse tous les points, y compris ceux des caractères ! Toutes les lettres se retrouvent donc à l’envers, voir figure 4.

[fichier SVG]

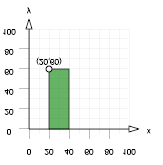
Figure 4: Inversion des
ordonnées et des caractères

Il faut donc soit les sortir du bloc de transformation et calculer leurs nouvelles coordonnées, soit leur appliquer de nouvelles transformations : scale(1,-1) permet de remettre à l’endroit les caractères. Mais elle fausse par la même occasion le calcul de coordonnées (x,y). Un caractère positionné sur le point P(20,60) se trouve après la première translation en un point P'(50,190) (grâce à la translation de (30,130)). Or il devrait se trouver à P''(50,70) soit 60 points plus haut que l’axe des abscisses (situé à y=130).

[fichier SVG]

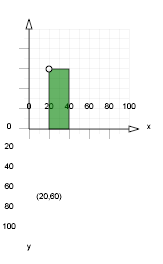
Figure 5: Remise à l’endroit
des caractères

Le point se trouve donc deux fois trop bas, voir figure 5. Une translation de -60 permet de le remonter sur l’axe des abscisses (y=0 dans le repère cartésien). Une seconde translation de -60 lui permet de trouver sa place (y=60 dans le répertoire cartésien). Il faut donc effectuer un translation pour tous les textes positionnées à (Xorig,Yorig) de (0, -2*Yorig). Maintenant que ces quelques règles sont établies, toutes les données du graphique résultat pourront être exprimées en coordonnées cartésiennes.

Collecter les informations avec python

La collecte des informations du système peut être réalisée à l’aide d’une fonction récursive. Les paramètres à lui fournir sont le nom de répertoire de base et la profondeur de parcours dans l’arbre du système de fichiers. La fonction va alors calculer le poids d’un répertoire donné et stocker dans une liste un tuple d’informations si le niveau du répertoire est compatible avec ce que veut l’utilisateur. Par exemple, l’appel de la méthode gatherSize(r"d:\monrep", 2), recueillera toutes les informations relatives à l’occupation disque du répertoire d:\monrep. Le second paramètre permet de fixer une limite en profondeur afin de synthétiser l’information. Ainsi, les données d’un répertoire d:\monrep\niv2 seront disponibles alors que les données d’un répertoire d:\monrep\niv2\niv3 ne le seront pas. Pour les avoir, il suffit de fournir le nombre adéquat à la méthode, soit 3.

L’utilisation de Python, de son support des tuples, des listes et des fonctions associées comme la somme, le filtrage ou les fonctions lambda permet d’écrire une méthode relativement courte et simple. La somme des tailles de chaque fichier contenu dans un répertoire donné. Pour cela, la fonction listdir récupère la liste de tous les éléments, fichiers et répertoires. Un filtre permet de ne garder que les éléments de type fichier (à l’aide de la fonction de test os.path.isfile). La fonction sum est utilisée pour calculer le poids de cette liste nouvellement créée.

def gatherSize(self, directory, level, deep=1):
listdir = os.listdir(directory)
filelist = filter(lambda
   f: os.path.isfile(os.path.join(directory, f)), listdir)
weight = sum([os.path.getsize(
   os.path.join(directory, name))
   for name in listdir])

Python et les listes

S’il y a bien un concept sur lequel Python est éclatant, c’est bien le support natif des listes. Les listes, les fonctions lambda, …(lire la suite)

Puis la même fonction gatherSize est appelée de façon récursive sur chacun des sous-répertoires. De la même façon que pour la liste des fichiers, la liste de répertoires peut être obtenue très simplement à l’aide d’un filtre. Puis, il suffit de faire la somme de toutes les tailles ainsi calculées pour obtenir le poids de la sous-arborescence. Celui-ci ajouté au poids de l’ensemble des fichiers du répertoire constitue le poids total du répertoire passé en paramètre de gatherSize.

subdir = filter(lambda f: os.path.isdir(os.path.join(directory, f)), listdir)
subdir_w = sum([self.gatherSize(os.path.join(directory,f),
                      level,deep+1) for f in subdir])
total = weight+subdir_w

Enfin, il faut déterminer si la profondeur n’est pas trop importante par rapport au besoin de l’utilisateur, et si les informations sont stockées ou non. Une fois le parcours arborescent terminé, les informations sont disponibles sous la forme d’une liste de couples (nom,taille) qui représente la liste des répertoires trouvés.

Production du SVG

Produire du SVG n’est pas compliqué en soi, une fois le système de représentation des coordonnées choisi. Comme il s’agit d’un format XML, plusieurs approches permettent de générer un tel flux. La première consiste à écrire directement le XML sans utiliser de librairie. Rapide à mettre en oeuvre, du moins au départ, la gestion des guillemets rend vite le code illisible et il faut faire attention à produire du XML bien formé. Seconde solution, utiliser les librairies XML, telle que dom, minidom (fournies en standard) ou une libraire tierce (4Dom ou ElementTree). Cette approche permet de produire un XML bien formé en utilisant un code plus clair. Enfin, il existe des API SVG pour python. Elles permettent de s’abstraire facilement de l’implémentation XML sous-jacente et de se concentrer sur les aspects SVG. Celle choisie dans cet article est SVGDraw. Ce n’est pas la plus complète ni la plus complexe, mais elle a l’avantage d’être très simple et de ne constituer qu’un seul fichier à mettre dans le répertoire site-package. Qui plus est, la version windows s’auto-installe. La création du document SVG se fait en deux étapes. La première va créer l’enveloppe globale. Une section déclarative, définie par l’élément SVG defs, contient trois motifs (éléments SVG pattern). Ils serviront à représenter la graduation des axes et la grille de fond. La figure 6 illustre le motif représentant l’axe des abscisses.

[fichier SVG]

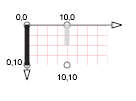
Figure 6: Motif pour la représentation des
graduations de l’axe des abscisses

Ce motif, d’une largeur de 20, définit deux traits verticaux. Le plus grand représentera toutes les graduations multiples de 20, le petit permettra d’identifier les graduations multiples de 10. Ces deux traits sont définis par des éléments SVG path. Outre les informations relatives au dimensionnement du motif et aux couleurs des traits, l’attribut le plus intéressant est la définition “d” du chemin. Elle consiste en une suite de commandes séparées par une virgule. Chaque commande est construite à l’aide d’une instruction désignée par une lettre (M,V,L,C,S,Q,T,...) et d’une ou plusieurs coordonnées (absolues ou relatives).

<pattern width="20"
   patternUnits="userSpaceOnUse"
   id="axeX" height="10">
   <path stroke="black"
         stroke-width="0.25"
         d="M 0 0, L 0 10" fill="none"/>
   <path stroke="lightgray"
         stroke-width="0.25"
         d="M 10 10, V 5" fill="none"/>
</pattern>

Le premier chemin est défini comme suit : Aller (M i.e Move) au point 0,0, faire une ligne (L i.e Lineto) jusqu’aux coordonnées absolues 0,10. La seconde ligne est définie par : Aller au point 10,10 et tracer une ligne verticale (V ou Vertical Lineto) jusqu’aux coordonnées absolues x,5 (la valeur de x ne change pas puisqu’il s’agit d’une ligne verticale). La spécification d’un attribut id=”axeX” permet de nommer ce motif et il pourra ensuite être utilisé de nouveau dans le graphique SVG, en faisant simplement référence à son nom. Le dessin de l’axe des x se fait donc ainsi :

<rect y="-10" width="240"
   fill="url(#axeX)" x="0" height="10"/>

Le rectangle est positionné plus bas que l’axe (avec des coordonnées cartésiennes), est large de 240 (le motif sera donc appliqué 12 fois) et est rempli avec le motif dont le nom correspond à “axeX”. Les motifs et les dessins effectifs de l’axe des Y et de la grille de fond sont construits sur le même principe.

Les lignes des axes sont dessinées à l’aide de l’élément SVG line et les deux flèches orientant les axes sont réalisées avec l’élément SVG polygon. Enfin, on affiche les informations générales sur le résultat de la recherche : le répertoire source et la taille globale utilisée. La seconde étape de la production du graphique va analyser chaque élément de la liste constituée dans la phase de collecte (voir ci-dessus) et ajouter un rectangle pour la représentation de la barre, et du texte pour afficher les informations relatives. On commence par trier la liste des couples (nom,taille). La taille occupée par le répertoire constitue le facteur de tri. Avec Python, le tri d’une liste constituée d’éléments complexes comme des tuples, des dictionnaires ou des objets se révèle très simple. Il suffit en effet de fournir une fonction de comparaison pour assurer l’opération :

def tupleCmp(self, a,b):
  (nameA, sizeA) = a
  (nameB, sizeB) = b
  return cmp(sizeB,sizeA)# tri des elements selon la taille occupee
self.infos.sort(self.tupleCmp)

Ici seules les tailles sont importantes, elles constituent donc le facteur de comparaison. Puisque c’est l’ordre décroissant qui nous intéresse, la fonction retournera donc 1 si sizeB>sizeA. Enfin, pour chaque élément de la liste, c’est à dire chaque répertoire, une barre est générée (via l’élément SVG rect) ainsi que deux zones de texte (éléments SVG text) : le pourcentage d’occupation et les informations sur le répertoire à proprement dit. Il suffit d’incrémenter à chaque fois l’axe des X, sans oublier d’ajouter les paramètres de transformation pour que les coordonnées cartésiennes exprimées dans la boucle soient cohérentes avec le système de coordonnées de SVG. Une fois, toutes les informations générées, le document SVG en mémoire est exporté vers un fichier XML temporaire. Le module webbrowser permet de lancer une instance du navigateur Internet avec l’URL du document ainsi construit. Le navigateur affiche alors le document SVG résultat. Il est donc nécessaire qu’il dispose du plugin approprié.

En une centaine de lignes de Python, nous avons pu analyser la structure d’un système de fichiers et produire un graphique vectorielle de haute qualité. Il serait simple de le rendre encore plus attractif en ajoutant d’autres éléments SVG. Par exemple, on pourrait obtenir un effet 3D des barres, ajouter une image dans la grille de fond, travailler les fontes avec des ombres, ou ajouter une dimension dynamique au graphique. Maintenant que les bases sont posées, libre à vous de laisser courir votre imagination…

Les sources de l’article

• stats.py
• l’archive des fichiers SVG
• Python SVGdraw